Interest rate changes bring uncertainty to fixed-income instruments like bonds. Duration and Convexity are two concepts that help investors to quantify the uncertainty.
Duration measures the sensitivity of the price of a bond due to a change in interest rate. Whereas convexity measures the change in yield and bond price due to a change in the interest rate. In other words, convexity measures the duration with a change in interest rate.
What is Duration?
Duration is used to measure the price of a bond with a change in interest rate changes. Bond prices, theoretically, move inversely to changes in interest rates.
Duration also measures the time it takes to recover a bond’s investment through its cash flows. It is the weighted average time of all cash flows in present value terms. Thus, it is also called effective maturity or average maturity of a bond.
Duration and Interest Rate Risk
Duration measures the time taken to recover a bond’s price from its cash flows. It also is a measure of the sensitivity of the bond’s price due to a change in interest rate. A bond with a longer duration will be prone to more price changes than a bond with a shorter duration.
Generally, if the interest rate changes by 1%, bond prices will change by 1% for each year remaining until the maturity date. If interest rates, for example, rise by 1% it will cause a 1% decrease in bond prices for every year until maturity. It means a bond with 3 years left to maturity will see a 3% reduction in its price. The converse for interest rate decline and bond price appreciation is also true.
Time to maturity and coupon rate are two key factors in duration measurement.
A bond with a longer maturity will take longer to cover its payment through cash flows. Thus, a bond with a longer duration will be more sensitive to interest rate changes than a bond with a shorter duration.
A bond with higher coupon rates will generate higher cash flows, thus recovering bond payment faster. It means a bond with a higher coupon rate will have a shorter duration and lower interest rate risk.
Formula
We can calculate the bond’s duration with the following formula.
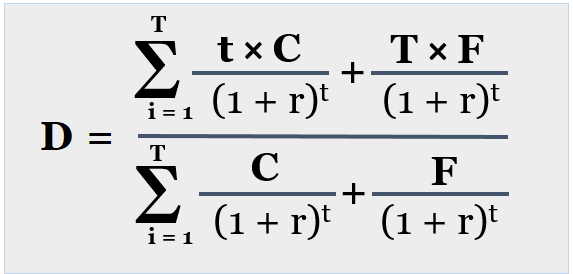
Where:
D = Macaulay’s Duration
T = number of periods until maturity
C = Period Coupon
r= periodic yield to maturity
i= ith time period
F = Face value of the bond
Modified Duration is a measure that estimates the percentage change in the price of the bond if the yield changes by 1%. We can calculate the modified duration by using the following formula.
Modified Duration = Macaulay’s Duration ÷ [1+(YTM/2)]
What is Convexity?
Theoretically, a change in interest rate risk is inversely proportional to the bond prices. It means the change in prices would reflect a straight line on the graph with changes in interest rate in either direction. Practically, many other factors contribute towards bond pricing and risk management, thus the relationship ends in a curve rather than a straight line.
Convexity is the measure of change in yield and the consequent bond prices. Duration is a fine concept if interest rate fluctuations are smaller and sudden. It can represent the relationship through a straight line. Convexity accommodates other risks factors that contribute towards the price sensitivity of the bond.
Convexity and Risk Management
If there are large interest rate changes and the bond has a longer maturity period, convexity is a better tool to measure the interest rate risk. A bond with a longer maturity period will be prone to more interest rate risks. Hence, it will be difficult to calculate price changes due to a change in interest rate.
A bond can have positive and negative convexity. If the duration of the bond increases with a rise in yield, it is said to have positive convexity. Contrarily, if the duration of the bond increases with a fall in the yield, it will have positive convexity.
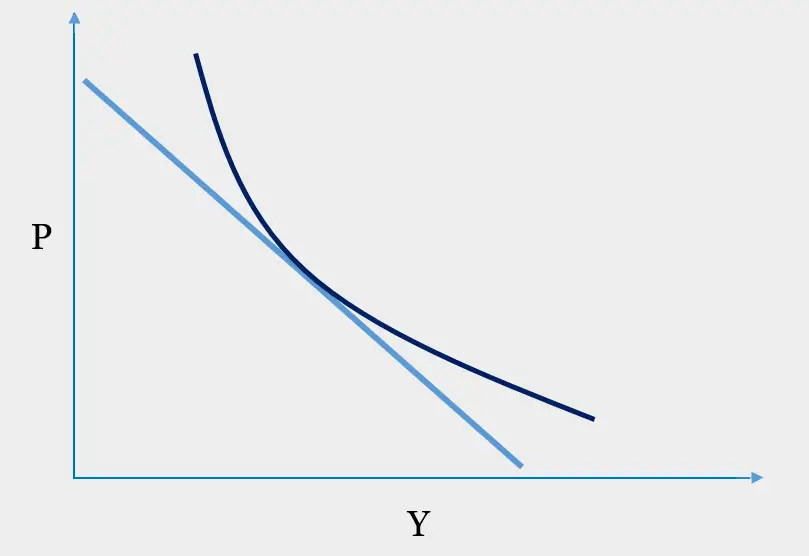
P = Price of the bond
Y= Yield on Maturity
The straight line represents the direct relation showing duration. Whereas the curvature denotes the relationship of yield and bond price sensitivity. It represents the convexity of the bond.
Convexity can be calculated with the following formula.
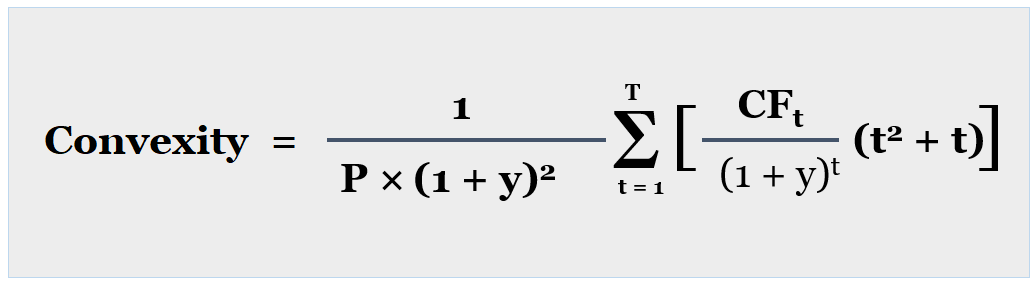
Generally, bonds with high yield rates will be less likely to get affected by interest rate changes. For instance, if a bond has a yield of 3% as compared to the market interest rate of 1%, it will be less likely to get affected by interest rate changes. It means the market interest rate would need to go above 3% to affect the YTM of this bond.
Thus, bonds with higher yields offer negative convexity and are less likely to get affected by interest rate changes. Contrarily, zero-coupon bonds will have higher convexity and will be affected quickly with interest rate changes.
Final Thoughts
Both duration and convexity are great tools for measuring interest rate risks with fixed-income securities such as bonds. Duration is used to measure the bond price sensitivity with a change in interest rate. Whereas convexity is a measure of bond prices with a change to yield to maturity of the bond. Both tools offer valuable information to investors and portfolio managers to mitigate interest rate risks on fixed-income securities.
