Real options in capital budgeting are one of the special forms for capital budgeting refinements. In a traditional procedure of the capital budgeting decisions without the real options, we simply apply any appropriate decision techniques; for instance, NPV or IRR and make the decision. Recently, the real options have emerged and it plays a vital technique in the modern view of capital budgeting decisions.
In this article, we cover what is real options in capital budgeting, different types as well as examples to calculate the value of real options.
What are Real Options in Capital Budgeting?
Real options are also known as strategic options. It is considered as the opportunities embedded in the investment projects that can provide additional value to the traditional capital budgeting decisions. In real options, it allows managers to alter their cash flows as well as risks so that it can possibly affect the acceptability of projects. In real options, we commonly use the Net Present Value (NPV) method in evaluating capital projects.
As mentioned above, real options in the capital budget are also called strategic options. This is because it allows managers or a company to make some changes or alter their cash flow decision when the opportunities come. This means that manager or company is able to make improved and more strategic decisions by considering the economic impact as a result of any contingent actions on the capital project cash flow and associated risk.
Major Types of Real Options in Capital Budgeting
There are 4 majors types of real options in capital budgeting. These are abandonment, option to expand, option to delay, and option to redeploy.
Abandonment Option or Option to Withdraw
This is the option to abandon or terminate any capital investment projects while the planned project life has not been completed. This strategic option allows avoiding minimize any losses encountered during the implementation of the project and it turns out to be bad. This is done by ceasing the project
In this abandonment option, the manager or company has the right but not the obligation to sell the project or cash flows for the remaining life of the project for salvage or scrap value. It often helps to increase the NPV when the management properly recognizes and accepts the abandonment option.
Option to abandon is like the American Put Options. The project or asset can be sold when the PV of the remaining cash flows falls below the liquidation value. Option to abandon is particularly important for capital intensive projects where a huge capital asset is needed. For instance, airlines, railroads, and nuclear plants, etc…
Option to Redeploy
Option to redeploy is also known as Flexibility Option. It is one type of real option that allows the company to use its existing production plant or assets one other activity other than the original one. This option is worthwhile when the PV from the cash flows of new project or activities exceed the costs of switching to the new projects or activities.
The option to redeploy is particularly important for the agricultural environment and utility industries. This is because for example, in an electric utility, we have the option to switch between various sources of fuel in order to produce electricity. In addition, the company has the choice of building either a plant or coal-fired plant in order to burn either coal or gas.
Option to Delay
Option to delay is one type of real options in capital budgeting that allows the firm to delay undertaking the projects at a later date. We can also call the option to delay as the Timing Option. Basically, in the traditional capital budgeting decisions, the firm just answers yes or no in accepting the project if it takes today. When the project is rejected today as a result of negative NPV or IRR is lower than the cost of capital, it does not mean it is not worthwhile or valuable. That is why the option to delay would be another technique to reconsider.
We can also call the option to delay as Call Options. The premium shall need to be paid to acquire the option on a given PV of the cash flows from operation in which the exercise price for this option is equal to the additional investment.
The value of option to delay is as follow:
NPV = PV – I, if PV > I, otherwise, NPV = 0
Where:
PV is the present value of cash flows
I is an additional investment.
Option to Expand
Option to expand is the option that allows a firm to put additional investment in the projects in the future or to enter new markets. We also call the option to expand as a Growth Option. In this option, the initial project would not be worthwhile to undertake. This is because it provides little or negative NPV. However, when there is an option to expand by injecting additional investment, the project would give a better and positive NPV. In this case, we may consider the initial investment as a premium to acquire the option to expand.
In the option to expand, the firm would only put an extra investment only if the project provides higher than the additional investment (I). This is when PV > I. However, if PV < I, the option to expand will not be undertaken.
Valuation of Real Options
In calculating the value of real options, we use the Black-Scholes Model; however, we need to apply certain adjustments. The Black-Scholes model is commonly used for the American Call Option, however since the principle of the American Call Option is similar to the real options, we can use the model to calculate the real options.
Even though the principle is similar, there are certain differences between the American Option and real options. The main difference is the estimation of volatility. This is because the underlying project under real options cannot be traded.
As mentioned in the above section, since the option to expand is a call option, then we can calculate the value of the option to expand by using the below formula:
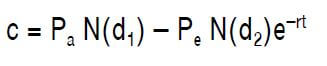
Where:
Pa is the value of the project
Pe is the additional investment for the expansion
Before we can calculate the call option, we first need to know d1 and d2 as follows:
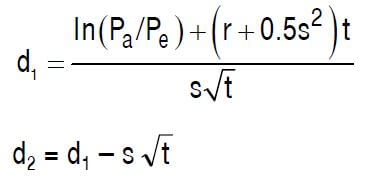
Then, we can calculate the put option which is the option to abandon as follows:
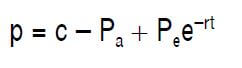
Example of Real Options
Assume that ABC Co is considering undertaking a 20 years project with an initial investment of $200 million in a real estate partnership with an American Real Estate Developer. This project would provide PV of expected cash flow of $198 million. This would create an NPV of $2 million throughout the project periods. ABC Co considers this NPV as a small amount and assumes further that ABC Co has the option to abandon this project anytime to sell its shares back to the American Developer in the next 5 years. The sales would be at $100 million.
A simulation of the cash flows for this project yields a variance of 0.09 as part of the PV of cash flow from being in the partnership. The risk-free rate for 5 years is 7%.
Calculate the real option to abandon this project.
Solution:
We can calculate the value of the real options of abandonment by using the Black-Scholes model as follows:
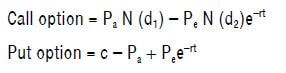
Where:
Pa = PV of cash flow from project = $200 million
Pe = $100 million which is the strike price or salvage value from abandonment
t = 5 years (the time to expiration of option)
s (Standard Deviation) = √0.09 = 0.3 (the variance in underlying asset’s value
r = 7%
Before calculating the value of option to abandon, we first need to calculate d1 and d2 as follow:
d1 = [In (200/100) + (7% + 0.5 × 0.32) × 5]/ (0.3 × √5)
d1 = [0.6931 + (0.115 × 5)]/ 0.6708 = 1.89
Then we can calculate d2 as follows:
d2 = d1 – s √ t
Hence, d2 = 1.89 – 0.3 × √5 = 1.22
By using the standard normal distribution table, we get the following:
N (d1) = 0.9767
N (d2) = 0.8888
Therefore, the value of call option is as follow:
Value of call option = 200 × (0.9767) – 100 × (0.8888) × e-0.07×5
Value of call option = 195.34 – 62.64 = $132.7 million
Therefore, we can calculate the value of put option as follows:
Put Option = 132.7 – 200 + (100 × e-0.07×5) = = $3.17 million
So the value of abandonment option is $3.17 million; therefore, we can add this amount with the original NPV of $2 million.
Hence, the total NPV including the abandonment option is $5.17 million. So, it is worthwhile to exercise the option to abandon as it creates a more than double NPV.
Conclusion
Real options in capital budgeting play a vital role in evaluating the project appraisal as it allows the firm to undertake the opportunities available. The real options contain 4 major types. These include the option to abandon, option to delay, option to deploy, and option to expand.
