When comes to unequal-lived and mutually exclusively projects, the annualized net present value is used as a decision rule for the project investment appraisal or capital budgeting decision or techniques. This is one of the capital budgeting refinements that we commonly encounter and use for the investment appraisal.
In this article, we cover in detail the annualized net present value. This includes the definition, the 3 step process how to calculate ANPV, using a spreadsheet to calculate the ANPV.
So let’s go through together!
Table of contents
What is the Annualized Net Present Value (ANPV)?
In capital budgeting refinements, there are three areas in which special forms of capital budgeting analysis are frequently used. These are capital rationing resulting from the binding of the budget constraint, recognition of real options, as well as the comparison of unequal-lived and mutually exclusive projects.
In this article, we cover only the comparison of mutually exclusive projects having unequal lives by using the annualized net present value approach.
The annualized Net Present Value (ANPV) approach is one of the capital budgeting decisions that is commonly used to evaluate mutually exclusive projects with different lives. It converts the net present value of unequal-lived projects into an equivalent annual present value.
By doing so, we can compare the net present value of unequal-lived projects so that the selection process can be done fairly. In the normal net present value method, the investment decision might not be properly carried out if there are mutually exclusive projects with unequal lives.
How to Calculate Annualized Net Present Value (ANPV)? 3 Step Process
In order to calculate the annualized NPV, we simply need to follow 3 step-process as follow:
Step 1: Calculate the NPV of each project being evaluated
Step 2: Divide the NPV as calculated in step 1 with the present value interest factor for an annuity at a given cost of capital in order to get the annualized NPV.
Below is the formula for the ANPV:
Annualized Net Present Value (ANPV) = NPV /PVIFA
Where:
NPV is the net present value of each project under evaluation
PVIFA is the present value of interest factor annuity
Step 3: Select the project with the highest annualized NPV
As mentioned above, when there are mutually exclusive projects with unequal lives, the normal NPV would provide a flawed result for capital budgeting decisions. Thus, we will illustrate the calculation by using both normal net present value as decision criteria and the ANPV as decision criteria.
Example
Suppose ABC Co is evaluating 2 projects; project A and B. Project A and B require the initial investment of US$50,000 and US$60,000 respectively. Below are the relevant cash flows of each project:
| Year | Project A US$ | Project B US$ |
|---|---|---|
| 1 | 20,000 | 30,000 |
| 2 | 28,000 | 25,000 |
| 3 | 35,000 | 20,000 |
| 4 | – | 19,000 |
| 5 | – | 13,000 |
| 6 | – | 8,000 |
The applicable cost of capital to use in evaluating these risky projects is 10%.
In order to clearly explain the difference between normal NPV and annualized NPV as a decision rule, we will illustrate the calculation for both normal NPV and ANPV.
Decision Rule Based on Normal NPV
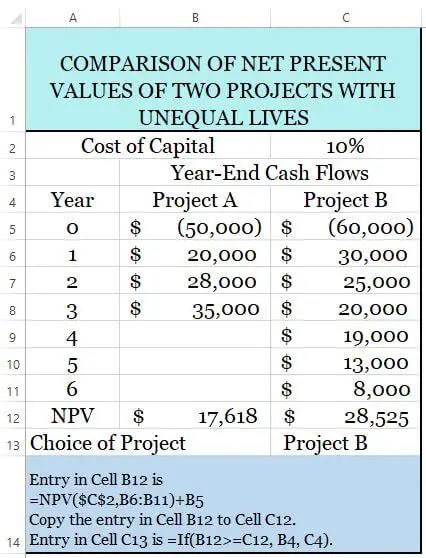
Now let’s do the calculation of the NPV for both projects based on the cost of capital of 10% given above.
We can illustrate this based on the table below:
| Year | Project A [a] | Project B [b] | PV factor at 10% [c] | PV Project A [d = a × c] | PV Project B [d = b × c] |
|---|---|---|---|---|---|
| 0 | (50,000) | (60,000) | 1.000 | (50,000) | (60,000) |
| 1 | 20,000 | 30,000 | 0.909 | 18,182 | 27,273 |
| 2 | 28,000 | 25,000 | 0.826 | 23,140 | 20,661 |
| 3 | 35,000 | 20,000 | 0.751 | 26,296 | 15,026 |
| 4 | 19,000 | 0.683 | 12,977 | ||
| 5 | 13,000 | 0.621 | 8,072 | ||
| 6 | 8,000 | 0.564 | 4,516 | ||
| NPV | 17,618 | 28,525 |
From the table above, by ignoring the differences in the project lives, both projects have positive NPV; thus it is worthwhile to invest. However, if ABC Co can only choose one project, thus ABC Co would prefer to choose project B because it provides the highest NPV as compare to project A.
On the other hand, if both project A and B are mutually exclusive, the difference in project lives would need to be reconsidered.
Decision Rule Based on ANPV
Due to the simple NPV is not the most efficient technique in evaluating the mutually exclusive projects with unequal lives, annualized NPV is the preferred approach.
We can take the NPV of both projects calculated above to further calculate the annualized NPV. The present value interest factor for projects A and B with the cost of capital of 10% is 2.487 and 4.355 respectively.
Therefore, we can calculate the ANPV by following the 3 step-process as follow:
Step 1: Calculate the NPV of each project being evaluated
The individual NPV of both projects A and B as calculated above are US$17,618 and US$28,525 respectively.
Step 2: Divide the NPV as calculated in step 1 with the present value interest factor for an annuity at a given cost of capital in order to get the ANPV
Below is the formula for the ANPV:
Annualized Net Present Value (ANPV) = NPV /PVIFA
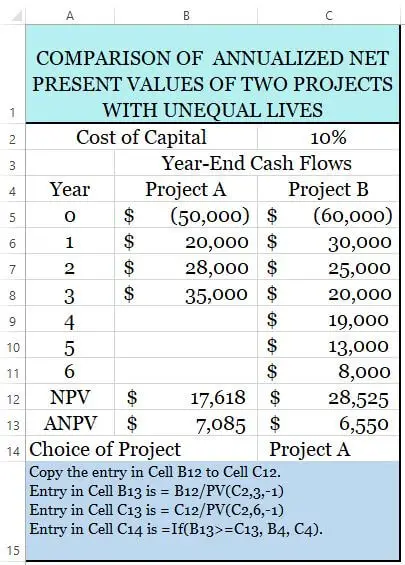
Based on the present value of the annuity, we get the PVIFA for project A of 2.487 and PVIFA for project B of 4.355. Therefore, we can calculate the ANPV as follow:
ANPV (A) = 17,618 / 2.487 = Us$7,085
ANPV (B) = 28,525 / 4.355 = US$6,550
Alternatively, we can calculate the ANPV as per the table below:
| Year | Project A | Project B |
|---|---|---|
| NPV [ a ] | 17,618 | 28,525 |
| PVIFA [ b ] | 2.487 | 4.355 |
| ANPV [ c = a / b ] | 7,085 | 6,550 |
Step 3: Select the project with the highest ANPV
In this last step, we need to select a project that provides the highest ANPV.
From the above table, the ANPV of project A is US$7,085 while project B has an ANPV of only US$6,550. Therefore, based on the ANPV decision rule, ABC Co would prefer to choose project A.
Spreadsheet Calculation of ANPV
We can also calculate the NPV and ANPV by using spreadsheets in Excel. Below is the sample spreadsheet calculation for both NPV and ANPV. You can follow the instruction of the formula at the bottom of each table.
Conclusion
Simple NPV is a good technique when comparing projects with the same lives; however, it is not efficient for mutually exclusive projects with different lives. Annualized NPV is the preferred approach for evaluating mutually exclusive projects with different lives.
